مطالب

در جلسه دوم از دوره‌ی مقدمه‌ای بر شبکه‌های عصبی بازگشتی (RNN) به بررسی دقیق‌تر اجزای تشکیل دهنده این شبکه‌ها یعنی واحد‌های بازگشتی و معادلات آن‌ها می‌پردازیم.

مرور

در جلسه اول دوره، با ماهیت و انواع شبکه‌های عصبی بازگشتی آشنا شده و فهمیدیم شبکه‌های RNN برای پردازش توالی‌ها و الگوهای متشکل از چندین مرحله استفاده می‌شوند. همچنین با استفاده از یک مثال ساده چراغ راهنمایی تفاوت این شبکه‌ها با شبکه‌های غیر بازگشتی را بررسی کردیم.

یک سلول/واحد بازگشتی

در شبکه‌های عصبی بازگشتی ورودی هر مرحله متشکل از دو قسمت است، یک ورودی مستقل از داده جاری همانند دیگر شبکه‌ها (عموما یک داده ترتیبی یا سری زمانی) و یک ورودی از خروجی مرحله‌ی قبل به‌عنوان حافظه‌ی نهان (Hidden State) که انتظار می‌رود مدل در این حافظه نهان، ویژگی‌هایی از داده‌های پردازش شده تا این مرحله را کد کرده و همانند یک حافظه نگه‌داری کند.

توجه به این نکته حائز اهمیت است که با وجود اینکه در این جلسات اولیه آموزش و در توضیح شبکه‌های عصبی بازگشتی و پردازش توالی داده‌ها تنها به این مورد اشاره می‌کنیم که شبکه از نتایج پردازش داده‌های قبلی برای تولید حافظه موقت خود استفاده می‌کند، اما شبکه‌های عصبی بازگشتی لزوما منحصر به این شرط نبوده و می‌توانند با روش‌های مختلفی از داده‌های بعدی (داده‌هایی که در آینده پردازش خواهند شد) نیز برای تولید حافظه استفاده کنند. این ویژگی به‌خصوص در پردازش‌های زبان طبیعی و ترجمه‌های ماشینی اهمیت داشته و استفاده می‌شوند.

پردازش واحد

به‌صورت کامل‌تر، سلول‌ها یا واحدهای بازگشتی اجزای تشکیل‌دهنده‌ای هستند که با تکرار آن‌ها (در طول دنباله‌‌ی داده‌های در حال پردازش) تشکیل یک شبکه عصبی بازگشتی می‌دهند. هر واحد بازگشتی متشکل از دو ورودی و یک خروجی به‌همراه وزن‌ها (Weights) و بایاس‌های (Biases) هرکدام است.

هر کدام از ورودی‌ها در وزن مربوطه خود ضرب شده و سپس به یکدیگر الحاق (Concatenate) شده (در کنار هم قرار گرفته) و به تابع فعال‌ساز (Activation Function) داده می‌شوند؛ نتیجه‌ی اعمال این تابع فعال‌ساز، خروجی واحدی خواهد بود که به‌عنوان حافظه‌ی نهان (Hidden State) شناخته شده و در مرحله بعد به‌همراه ورودی استفاده می‌شود.

ابعاد حافظه نهان (Hidden State)

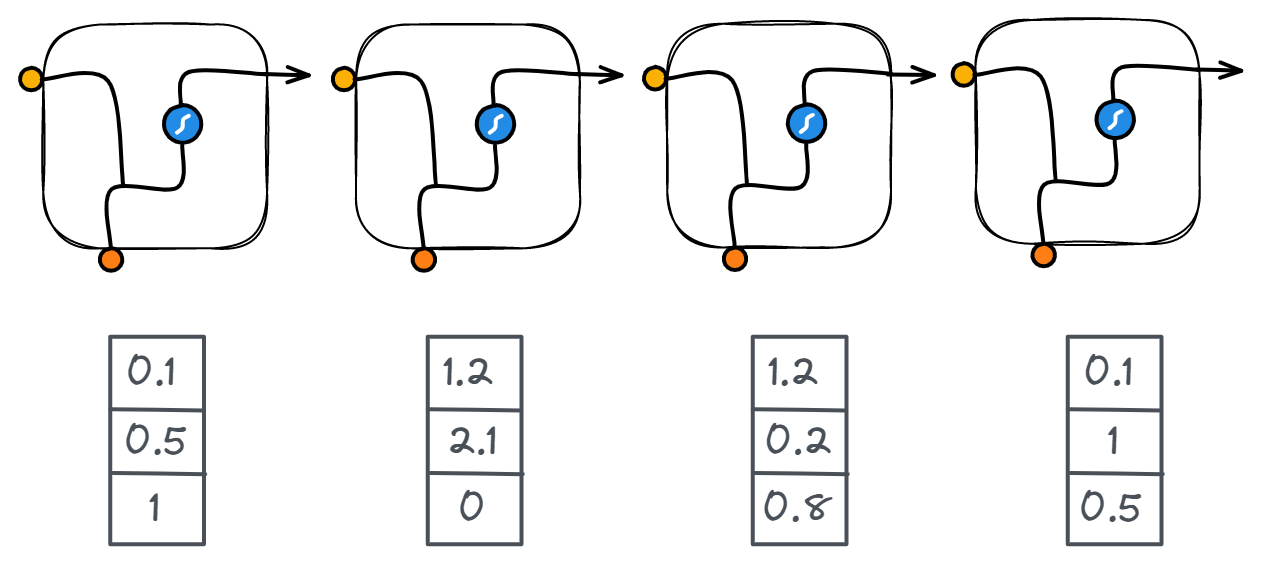
طول بردار حافظه نهان (Hidden State) ثابت نبوده و خود یک ابر پارامتر (Hyper Parameter) است و همانند باقی ابر پارامترها با یک بردار مقادیر تصادفی (Random) و یا بردار صفر (برداری که تمام المان‌هایش صفر هستند) مقداردهی اولیه می‌شود.

مدل ذهنی

برای درک درست نحوه‌ی کار شبکه‌های عصبی بازگشتی، نیاز است تا ساختار و مدل ذهنی (Mental Model) درستی از واحد‌های بازگشتی و نحوه قرارگیری و استفاده آن‌ها داشته باشیم که البته در طول دوره و با یادگیری جزئیات بیشتر این مدل ذهنی را توسعه می‌دهیم.

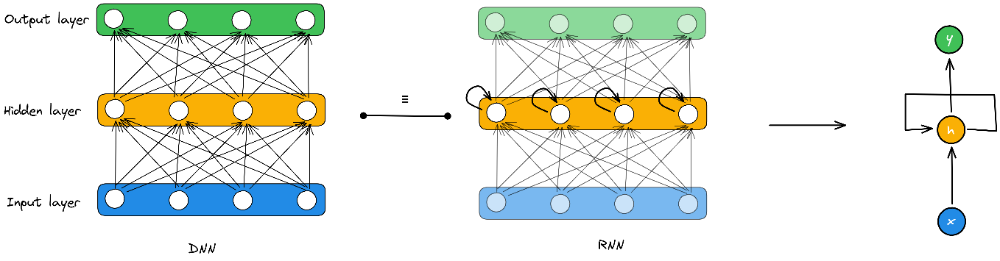
توجه کنید که هرچند که به این اجزای سازنده‌ی شبکه‌های بازگشتی، سلول نیز گفته می‌شود، تصور و برداشت از آن‌ها نباید محدود به یک واحد پردازش ساده باشد؛ برای مثال، در تصویر زیر مقایسه‌ای از یک شبکه‌ی تمام-متصل و یک شبکه‌ی بازگشتی معادل را مشاهده می‌کنید که در آن گره‌ها در لایه‌های مختلف یک شبکه‌ی عصبی، فشرده شده و تشکیل یک واحد عصبی بازگشتی می‌دهند [1]:

توالی و باز کردن واحدها

در نمایش، شبکه‌های بازگشتی معمولاً به‌صورت یک واحد بازگشتی که Hidden State خروجی آن به Hidden State ورودی متصل است، مصور می‌شود. در مقابل می‌توان این شبکه را در طول زمان باز کرده (unroll) و آن را به‌صورت دفعات اجرای مختلف نمایش داد که در هر مرحله، ورودی مربوط به Hidden State آن مرحله، از Hidden State خروجی مرحله‌ی قبل استفاده شده است [2].

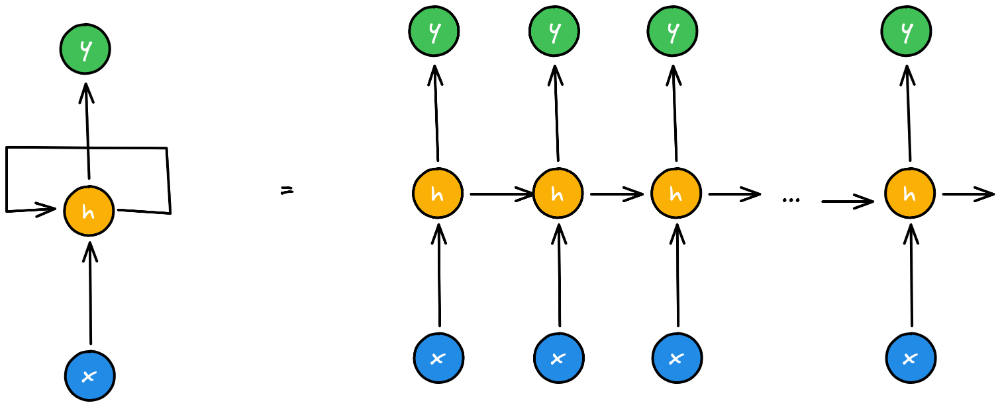
مشخص است در هر مرحله از اجرای شبکه، یک واحد یکسان (یک شبکه یکسان) استفاده می‌شود. این بدین معنی است که وزن‌ها و بایاس‌های مورد استفاده واحد بازگشتی در هر بار اجرا بروزرسانی می‌شوند.

خروجی واحد

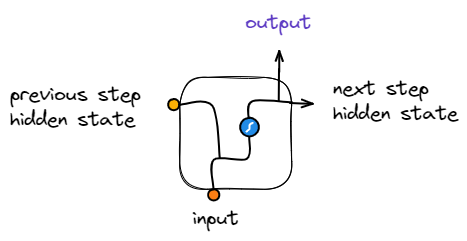
برای خروجی گرفتن از شبکه، یک انشعاب از Hidden State خروجی هر سلول جدا می‌کنیم. این انشعاب در ادامه بسته به‌نوع مسئله به یک شبکه دیگر متصل می‌شود. برای مثال، برای یک وظیفه (Task) طبقه‌بندی چند-کلاسه خروجی هر واحد به یک شبکه تمام-متصل با تابع فعال‌ساز بیشینه هموار (Softmax) متصل خواهد شد.

تابع فعال‌ساز

در شبکه‌های ساده عصبی بازگشتی معمولا از تابع tanh (تانژانت هذلولی) به‌عنوان تابع فعال‌ساز استفاده می‌شود. tanh تابعی سیگموئید (Sigmoid) بوده تمامی مقادیر ورودی را بین -1 تا 1 نگاشت می‌کند. این تابع به‌صورت زیر تعریف می‌شود و نمودار آن قابل رسم است [2]:

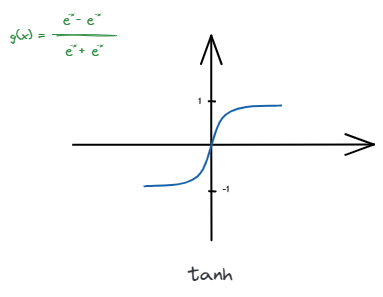
ویژگی این تابع این است که تمامی ورودی‌ها در بازه ثابتی نگاشت شده و این امکان را می‌دهد تا ورودی‌های بزرگ خیلی پراهمیت و ورودی‌های کوچک خیلی کم‌اهمیت نشوند. در واقع نسبت تاثیر ورودی‌ها را متعادل کرده و باعث بهبود عملکرد مدل می‌شود.

نشانه‌گذاری و معادلات

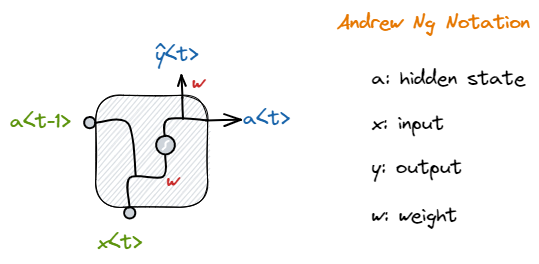
می‌توانیم روابط ریاضی میان ورودی و خروجی‌های یک سلول بازگشتی را به‌صورت ضرب‌های ماتریسی فرمول‌بندی کنیم. در این آموزش برای راحتی و سازگاری از قواعد نشانه‌گذاری (notation) پروفسور Andrew Ng استفاده می‌کنیم. در این نشانه‌گذاری علائم به‌صورت زیر تعریف می‌شوند:

• x بردار ورودی واحد
• ^y بردار خروجی واحد
• a بردار حافظه نهان یا Hidden State
• w ماتریس وزن

برای مثال، شبکه عصبی بازگشتی ساده‌ای به‌صورت باز (unroll) شده زیر در نظر بگیرید:

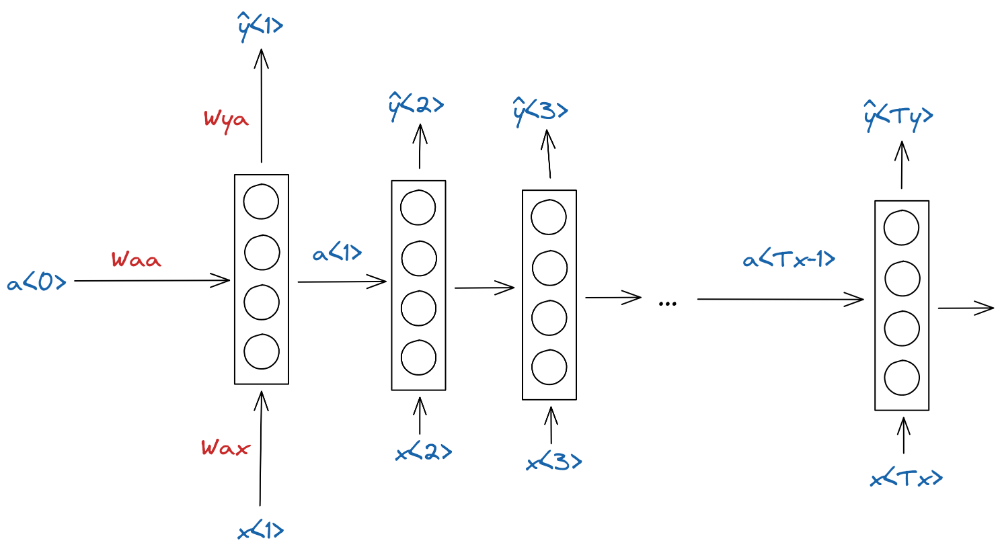
در این شبکه، ورودی سلول در هر مرحله x(t) در وزن Wax (وزن تولیدکننده a و ضرب‌شونده در x) و Hidden State هر مرحله a(t) نیز در وزن Waa (وزن تولیدکننده a و ضرب شونده در a) ضرب می‌شوند. سپس از الحاق نتایج این دو ضرب و اعمال تابع فعال‌سازی (G1 [tanh]) بر آن، Hidden State جدید تولید می‌شود. در ادامه، می‌توان برای گرفتن خروجی، Hidden State به‌دست آمده را در یک وزن Wya (وزن تولیدکننده y و ضرب‌شونده در a) ضرب کرد. 

معادلات اولیه

با توجه به توضیحات بالا، می‌توان این ضرب‌های ماتریسی را به‌صورت معادلات زیر خلاصه کرد:

معادله حافظه نهان (Hidden State) هر مرحله

مطابق این معادله، Hidden State در هر مرحله برابر است با اعمال یک تابع فعال‌ساز مانند G1 بر حاصل جمع، ضرب ورودی و Hidden State مرحله قبل، بر وزن‌هایشان و باباس.

معادله خروجی هر مرحله

خروجی نیز برابر اعمال تابع فعال‌ساز دیگری (G2) بر حاصل‌جمع، ضرب Hidden State محاسبه‌شده مرحله جاری در وزن مربوطه و بایاس خواهد بود.

معادلات ساده‌شده

برای ساده‌ترکردن محاسبات و قواعد نشانه‌گذاری، می‌توان بردارهای ورودی و Hidden State را الحاق کرده و تنها از یک وزن با نام Wa برای آن استفاده کنیم. طبیعی است دراین‌صورت ابعاد این ماتریس وزن تغییر کرده و برابر با [طول ورودی, طول حافظه نهان] خواهد بود. همچنین برای وزن تشکیل دهنده خروجی نیز از نام Wy استفاده می‌کنیم.

نحوه انجام الحاق‌ها

برای بررسی ابعاد بردارها و ماتریس‌های هر واحد، مثال زیر را در نظر بگیرید:

فرض‌کنید می‌خواهیم مدلی برای پردازش کلمات بسازیم؛ می‌دانیم که طول حافظه نهان (Hidden State) ما یک ابر پارامتر بوده و اختیاری‌ست، در این مثال برای آن مقدار 100 المان را در نظر می‌گیریم. اما، بردار ورودی‌ها به مسئله وابسته بوده و در این مثال یک بردار وان هات (One Hot) مثلا یک دیکشنری از کلمات و برداری به طول 10000 المان را در اختیار داریم.

از آنجایی که خروجی هر مرحله یک بردار 100تایی خواهد بود (چون طول بردارِ Hidden State را برابر 100 در نظر گرفتیم)، در این صورت طول ماتریس‌های وزن‌ Waa و Wax به‌صورت زیر خواهند بود:

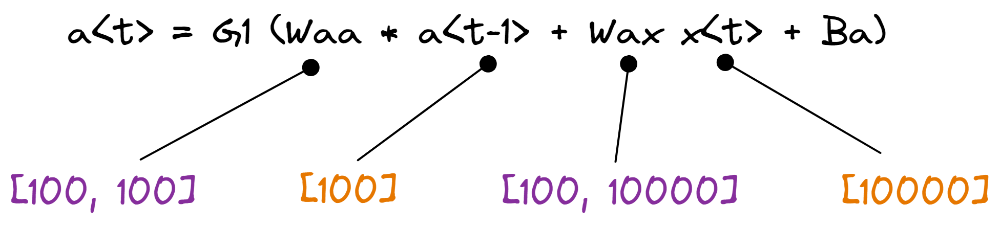
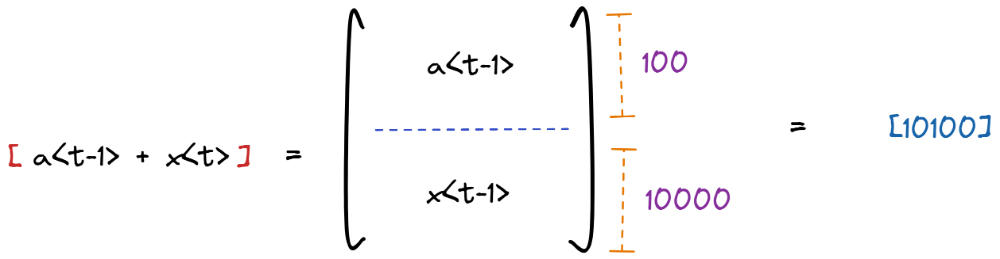
الحاق بردارهای a و x
بردارهای ورودی هر مرحله و حافظه نهان (Hidden State) را به‌صورت عمودی به یکدیگر الحاق می‌کنیم تا در نهایت یک بردار از مجموعه طول‌های آن‌ها (در مثال ما 10100 المان) داشته باشیم:

الحاق ماتریس‌های Wax و Waa
همچنین، ماتریس‌های وزن‌های مربوط به ورودی هر مرحله و حافظه نهان (Hidden State)، یعنی به‌ترتیب Wax و Waa را به‌صورت افقی به یکدیگر الحاق می‌کنیم تا در نهایت یک ماتریس به ابعادِ [طول ورودی, طول حافظه نهان] (در مثال ما [10100, 100]) داشته باشیم:

.    .    .    .    .

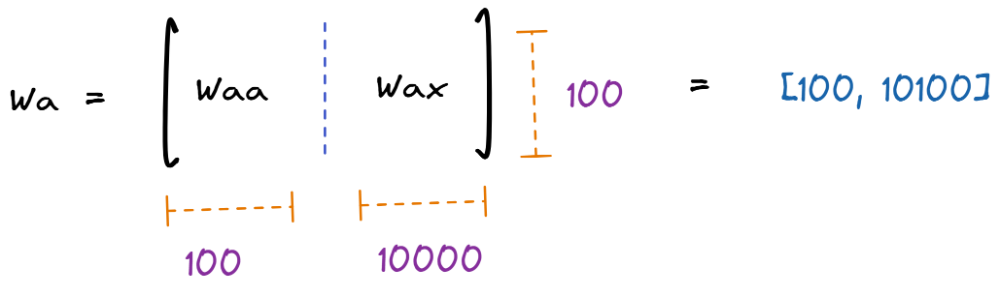
در این جلسه در ادامه مباحث جلسه‌ی قبل، به بررسی دقیق‌تری از واحدهای بازگشتی، اجزای اصلی تشکیل‌دهنده شبکه‌های عصبی بازگشتی پرداختیم و فهمیدیم ورودی‌ها و خروجی‌های هر واحد چیست و چگونه تشکیل می‌شود، به‌علاوه با معادلات ماتریسی آن‌ها آشنا شده و قواعد نشانه‌گذاری استاندارد آن را مرور کردیم.

در جلسه‌ی بعدی یک شبکه عصبی بازگشتی ساده برای تخمین یک تابع سینوسی پیاده‌سازی می‌کنیم.

می‌توانید لیست جلسات دوره را در این پست مشاهده کنید.

• جلسه‌ی قبلی
• جلسه‌ی بعدی

این دوره به کوشش علی‌رضا اخوان‌پور به‌صورت ویدئویی تهیه شده و به قلم محمدحسن ستاریان با نظارت ایشان به‌صورت متنی نگارش و توسط بهار برادران افتخاری ویرایش شده‌ست.

در صورت تمایل به خرید دوره به صورت ویدئویی می‌توانید با استفاده از کد تخفیف shenasablog_rnn2 از 20 درصد تخفیف بهره‌مند شوید.

منابع

در انتهای هر پاراگراف این پست شماره‌ی منبع یا منابعی که در نگارش آن قسمت از آن‌ها کمک گرفته شده ذکر شده، در لیست زیر می‌توانید هر کدام از این منابع را مشاهده و مطالعه کنید:

[1] آموزش‌های simplilearn

[2] آموزی‌های IBM Cloud