مطالب

در جلسهٔ سوم از دوره‌ی مقدمه‌ای بر شبکه‌های عصبی بازگشتی (RNN) به پیاده‌سازی یک شبکه‌ی RNN ساده با استفاده از کتابخانه کراس (Keras) می‌پردازیم.

مرور

در جلسهٔ اول دوره، با ماهیت و انواع شبکه‌های عصبی بازگشتی آشنا شده و فهمیدیم شبکه‌های RNN برای پردازش توالی‌ها و الگوهای متشکل از چندین مرحله استفاده می‌شوند. در جلسهٔ دوم به سلول‌های بازگشتی پرداخته و همچنین معادلات مربوط به آن‌ها را بررسی کردیم.

مقدمه

در این جلسه به پیاده‌سازی یک شبکه عصبی بازگشتی ساده با استفاده از کتاب‌خانه کراس (Keras) پرداخته و این شبکه را برای پیش‌بینی روند یک تابع سینوسی آموزش می‌دهیم و عملکرد آن را بررسی می‌کنیم. پیش‌بینی روند تابع که یک تسک از نوع رگرسیون (Regression) می‌باشد، عموما نیازمند حافظه‌ای‌ست که بتواند توسط آن روند کلی پیشرفت تابع را درک کند، از این رو شبکه‌های عصبی بازگشتی انتخاب مناسبی برای این تسک‌ است.

دسترسی به کدها

برای مشاهده و دریافت کدهای این جلسه می‌توانید از طریق محزن گیت‌هاب فایل نوت‌بوک را دریافت کرده و یا از طریق این لینک به‌صورت آنلاین مشاهده کنید. برای اجرای نوت‌بوک‌ به‌صورت آنلاین و رایگان می‌توانید از طریق لینک زیر نوت‌بوک را در سرویس Google Colab اجرا کنید:

اجرا:‌ باز کردن نوت‌بوک در Google Colab

پیاده‌سازی شبکهٔ بازگشتی ساده (SimpleRNN)

در ابتدا کتابخانه‌های مورد نیاز خود را import می‌کنیم:

import pandas as pd
import numpy as np

import matplotlib.pyplot as plt

from keras.models import Sequential
from keras.layers import Dense, SimpleRNN

سه خط اول این تکه کد مربوط به وارد کردن کتابخانه‌های استانداردی‌ست که در اکثر برنامه‌های خود استفاده می‌کنیم:

• کتابخانه pandas برای کار با داده‌ها
• کتابخانه numpy برای کار با ماتریس‌های چند-بعدی و تنسورها (Tensor)
• کتابخانه‌ matplotlib برای ترسیمات و نمودارها

همچنین از کتاب‌خانه‌ی کراس (Keras)، کلاس sequential (ساخت مدل به‌صورت لایه-لایه) و از keras.layers علاوه‌بر شبکه‌ی Dense (برای پیاده‌سازی شبکه‌های تمام-متصل) در اینجا SimpleRNN را نیز برای پیاده‌سازی شبکه‌های عصبی بازگشتی وارد می‌کنیم.

ایجاد مجموعه داده

برای آموزش مدل از یک تابع سینوسی ساده که مقداری نویز بر آن اعمال شده استفاده می‌کنیم. برای ایجاد این مجموعه‌داده‌، به‌صورت زیر خروجی یک تابع سینوسی را به‌ازای ورودی‌های 0 تا 1500 (1500 گام زمانی [timestep]) ذخیره می‌کنیم.

t = np.arange(0,1500)
x = np.sin(0.02*t)+ np.random.rand(1500) * 2
plt.plot(x)
plt.show()

نحوه‌ی پیاده‌سازی تابع اهمیت چندانی ندارد، مهم خروجی تابع است که در نمودار زیر قابل مشاهده است:

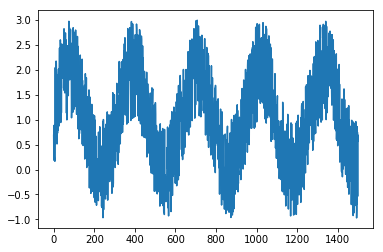
در ادامه بررسی خواهیم کرد که آیا مدل بازگشتی ساده‌ی ما قادر به ادامه دادن روند تابع (با مشاهده‌ی روند قبلی تابع) است یا خیر.

جدا کردن داده‌های آموزشی و آزمون

پیش از این برای آموزش شبکه‌های تمام-متصل (fully-connected یا Dense)، برای تقسیم مجموعه داده به دیتاست‌های آموزش (Train) و آزمون (Test) داده‌ها را بُر زده (Shuffle) و به‌صورت تصادفی (Random) داده‌ها را جدا می‌کردیم.

برای آموزش شبکه‌های عصبی بازگشتی، از آنجایی‌که هدف یادگیری یک سری زمانی‌ست؛ باید بسته به نوع مسئله، فرایندی برای جدا کردن داده‌های آموزش و آزمون انتخاب کنیم. این فرایند‌ها را می‌توانیم با بررسی مسائل مختلف و تجربه کردن یاد بگیریم.

در مسئله پیش‌رو، بدین صورت عمل می‌کنیم که از 1500 گام زمانی‌ای که در مجموعه‌داده‌ی ساختگی خود تولید کردیم، تعدادی (برای مثال 1000 گام اول) را به‌عنوان ورودی شبکه در نظر گرفته و برای فاز آموزش استفاده می‌کنیم و تعداد باقی‌مانده (برای مثال 500 گام آخر) را به‌عنوان خروجی مورد انتظار شبکه در نظر گرفته و برای فاز تست استفاده می‌کنیم.

برای تقسیم مجموعه‌داده به دو مجموعه‌ی داده‌های آموزش و داده‌های آزمون به‌صورت زیر عمل می‌کنیم:

train, test = x[0:1000], x[1000:]

در اینجا 1000 داده ابتدایی مجموعه داده اصلی را به‌عنوان داده آموزش و مابقی را به‌عنوان داده آزمون جدا کرده‌ایم.

آماده‌سازی داده و ایجاد ورودی (Input) و برچسب (Label)

همانطورکه در جلسه‌ی قبل خواندیم، شبکه‌های عصبی بازگشتی از تکرار (به‌اصطلاح در کنار هم قرار گرفتن) یک واحد بازگشتی (سلول بازگشتی) تشکیل می‌شوند. برای مثال از کنار هم قرار گرفتن پنج سلول، پنج گام زمانی (timestep) و از کنار هم قرار گرفتن 100 سلول، 100 گام‌زمانی خواهیم داشت. در خیلی از مسائل، این که مسئله را در چند گام‌زمانی باز کنیم خود یک ابرپارامتر (Hyper Parameter) است.

به‌بیان‌دیگر، ورودی شبکه‌های عصبی بازگشتی (RNN) دنباله‌هایی از داده‌ها مانند سری‌های زمانی هستند. برای آموزش مدل، در هر مرحله، دنباله‌هایی از داده‌های آموزش و برچسب آن (خروجی مورد انتظار) به شبکه خوراک می‌شوند؛ اینکه طول هر دنباله ورودی به چه اندازه باشد، به مسأله و داده‌های موجود جهت حل آن بستگی دارد و یک ابرپارامتر است.

ابرپارامتر (Hyper Parameter) بودن طول دنباله‌ی ورودی (input)، بدین معنی‌ست که مقدار بهینه از پیش مشخصی ندارد. برای انتخاب مقدار مناسب یک ابرپارامتر می‌توانیم در دوره‌های متوالی آموزش مدل، آن را تغییر داده و نتیجه‌ی این تغییرات را در عملکرد مدل بررسی کنیم.

x = [1,2,3,4,5,6,7,8,9,10]

برای آموزش شبکه عصبی بازگشتی، ورودی‌ها و خروجی‌ها را به‌صورت یک دنباله‌ ورودی و برچسب (خروجی مورد انتظار، در اینجا عنصر بعدی) به شبکه می‌دهیم. مثلا اگر طول دنباله ورودی را یک در نظر بگیریم، در هر مرحله ورودی و برچسب به‌صورت زیر خواهد بود:

x  y
1 2
2 3
3 4
4 5
..
9 10

در اینجا تنها یک گام‌زمانی (timestep) داشته و تنها از تکرار یک واحد بازگشتی استفاده کردیم. بدین صورت در هر مرحله، از شبکه بازگشتی انتظار داریم با دیدن یک ورودی، خروجی بعدی را پیشنهاد بدهد.

همچنین اگر طول را سه در نظر بگیریم، خواهیم داشت:

x        y
1,2,3 4
2,3,4 5
3,4,5 6
4,5,6 7
...
7,8,9 10

در این حالت سه گام‌زمانی (timestep) داشته و واحد بازگشتی سه بار تکرار شده‌ است؛ دراین‌صورت، در هر مرحله از شبکه بازگشتی انتظار داریم با دیدن دنباله‌ای از سه ورودیِ گذشته، خروجی بعدی را پیش‌بینی کند.

طول دنباله ورودی، در واقع نشان‌دهنده‌ی تعداد گام‌های زمانی‌ای است که واحد بازگشتی را تکرار می‌کنیم یا به‌اصطلاح مدل را به این تعداد گام‌زمانی (timestep) باز می‌کنیم.

.    .    .    .    .

در ادامه‌ی پیاده‌سازی برنامه‌ی پیش‌بینی تابع سینوسی، تعداد گام‌های زمانی را برابر 10 قرار می‌دهیم (متغیر step) و داده‌های آموزش و آزمون را به فرمت مورد انتظارِ شبکه (فرمتی از آرایه‌های ورودی و برچسب آن‌ها که بالاتر توضیح داده شد) در می‌آوریم.

در اینجا برای سهولت ایجاد دنباله‌های ورودی و برچسب هرکدام، تابع کمکی‌ای (helper function) به‌نام convertToDataset نوشته و استفاده شده است:

step = 10

# convert into dataset data and label
def convertToDataset(data, step):
    # data = np.append(data, np.repeat(data[-1,], step))
    X, Y = [], []
 for i in range(len(data) - step):
        d = i + step  
        X.append(data[i:d,])
        Y.append(data[d,])
 return np.array(X), np.array(Y)

trainX, trainY = convertToDataset(train, step)
testX, testY   = convertToDataset(test, step)

پس در نهایت داده‌های آموزش ما، یعنی trainX و testX لیست‌هایی 10تایی خواهند بود که هر کدام از آن‌ها با نمونه‌ی بعدی در 9 خانه همپوشانی دارند. (9 المان از هر دو عنصر متوالی لیست برابر هستند) برای بررسی ابعاد داده‌ها به‌صورت زیر عمل می‌کنیم:

print(trainX.shape)
print(testX.shape

نتیجه آن به‌صورت زیر خواهد بود:

(990, 10)
(490, 10)

تغییر ابعاد داده‌ها برای ورودی‌دادن به شبکه

پیش از دادن ورودی‌ها به شبکه، نیاز است تا ابعاد آن‌ها به‌صورتی که مورد انتظارِ کتاب‌خانه‌ی Keras است تغییر کند. ورودی شبکه RNN ساده در کتاب‌خانه‌ی کراس به‌صورت زیر است:

(NumberOfSequences, TimeSteps, ElementsPerStep)

• NumberOfSequences تعداد داده‌های ورودی (در اینجا 990 نمونه). این مورد معادل NumberOfSamples در شبکه‌های تمام‌متصل است.
• TimeStep تعداد گام‌های زمانی در هر ورودی (در اینجا 10). برابر تعداد دفعاتی که شبکه بازگشتی unroll می‌شود.
• تعداد فیچر‌های هر نمونه (در اینجا 1 چرا که هر المان تنها یک عدد است).

برای تغییر ابعاد نمونه‌های مجموعه‌داده‌های آموزش و آزمون به‌صورت زیر عمل می‌کنیم:

# trainX.shape = (990, 1) | testX.shape = (490,, 1)
trainX = np.reshape(trainX, (trainX.shape[0],  trainX.shape[1], 1))
testX = np.reshape(testX, (testX.shape[0],testX.shape[1], 1))

بدین‌صورت ابعاد داده‌ها به‌صورت زیر در خواهد آمد که مورد انتظار کتاب‌خانه کراس (Keras) است:

(990, 10, 1)
(490, 10, 1)

ساخت مدل (تعیین معماری شبکه و کامپایل آن)

در کتاب‌خانه کراس می‌توانستیم مدل‌ها را به‌طریق Sequential یا Model Subclassing و یا توسط Functional API بسازیم. در اینجا به‌دلیل سادگی کار از روش Sequential استفاده می‌کنیم. قطعه کد زیر را ببینید:

model = Sequential()
model.add(SimpleRNN(units=64, activation="tanh"))
model.add(Dense(1))
model.compile(loss='mean_squared_error', optimizer='rmsprop')

پس از تعریف مدل به‌صورت Sequential، یک لایه SimpleRNN به ساختار مدل اضافه می‌کنیم. هر لایه simpleRNN حداقل یک آرگومان units دریافت می‌کند که بیانگر سایز حافظه‌ی نهان لایه بازگشتی بوده (تعداد نورون‌های واحد بازگشتی) و یک ابرپارامتر است.

در ادامه، در لایه simpleRNN به‌عنوان تابع فعال‌ساز (Activation Function) از تابع tanh که جلسه پیش بررسی کردیم استفاده می‌کنیم.

سپس از آنجایی‌که در هر گام‌زمانی (timestep) می‌خواهیم مقدار تابع سینوس را، که یک عدد واحد است، پیش‌بینی کنیم؛ یک لایه تمام-متصل (Dense) با تنها یک نورون برای تعیین خروجی شبکه اضافه می‌کنیم.

در نهایت مدل را با استفاده از دستور compile با تعیین تابع زیان mean squared error ( تابع زیانی به‌صورت معمول در تسک‌های رگرسیون استفاده می‌شود) و optimizer تعیین شده کامپایل می‌کنیم.

بررسی ساختار مدل (Model summary) - قسمت اول

به‌عنوان یک نکته‌ی جانبی، آیا پس از کامپایل مدل و در مرحله‌ی فعلی می‌توانیم با استفاده از متد model.summary ساختار مدل را بررسی کنیم؟ دانستن این نکته در جلسه‌ی آینده اهمیت خواهد داشت.

برای تست این مسأله دستور زیر را اجرا می‌کنیم:

model.summary()

اگر دستور بالا را (در مرحله فعلی و همگام با این جلسه) اجرا کنید ساختار مدل قابل مشاهده نخواهد بود و اخطاری دریافت خواهیم کرد با این عنوان که یا مدل Build نشده یا سایز ورودی مشخص نیست. بنابراین برای دریافت ساختار مدل نیازمند حداقل اطلاعاتی از ورودی شبکه هستیم.

با این‌حال می‌توانیم مدل را روی دیتای خود آموزش داده و fit کنیم.

آموزش مدل

برای آموزش مدل روی داده‌های آموزشی که ایجاد کردیم به‌صورت زیر عمل می‌کنیم:

history = model.fit(trainX, trainY, epochs=100, batch_size=16, verbose=2)

در اینجا داده‌های ورودی فاز آموزش (trainX) و برچسب‌های آن‌ها (trainY) را به مدل معرفی کرده و در 100 دوره (Epoch) مدل را آموزش می‌دهیم. برای ورودی دادن به مدل سایز دسته‌ها (Batch Size) را برابر 16 گذاشته و با استفاده از آرگومان verbos = 2 تعیین می‌کنیم اطلاعات مرحله آموزش مدل تا چه اندازه چاپ شود.

پس از اجرای این مرحله -که می‌تواند تا چند دقیقه طول بکشد- خروجی زیر را خواهیم داشت. برای سهولت تنها چند دوره (Epoch) آخر را در زیر می‌بینیم:

...

Epoch 95/100
 - 1s - loss: 0.1231
Epoch 96/100
 - 1s - loss: 0.1245
Epoch 97/100
 - 1s - loss: 0.1151
Epoch 98/100
 - 1s - loss: 0.1133
Epoch 99/100
 - 1s - loss: 0.1130
Epoch 100/100
 - 1s - loss: 0.1077

همانطور که قابل مشاهده‌ست، مدل در Mini Batch آخر به زیان (Loss) برابر 0.1.7 نزدیک شده.

بررسی ساختار مدل (Model summary) - قسمت دوم

در قسمت اول بررسی ساختار مدل و پیش از آموزش مدل دیدیم که نمی‌توانیم با استفاده از دستور model.summary ساختار مدل را بررسی کنیم. آیا الان و پس از آموزش می‌توانیم؟ با اجرای دستور زیر این مورد را بررسی می‌کنیم:

model.summary()

با اجرای متد فوق، توپولوژی شبکه به‌صورت زیر قابل مشاهده خواهد بود:

Model: "sequential"
_________________________________________________________________
Layer (type)                 Output Shape              Param #   
=================================================================
simple_rnn (SimpleRNN)       (None, 64)                4224 
_________________________________________________________________
dense (Dense)                (None, 1)                 65 
=================================================================
Total params: 4,289
Trainable params: 4,289
Non-trainable params: 0
_________________________________________________________________

این نکته قابل توجه است که با وجود اینکه در هنگام تعریف لایه‌های شبکه، سایز ورودی‌های مدل را به‌صورت مشخص به مدل ندادیم، اما پس از آموزش مدل و fit کردن، مدل با دریافت ابعاد داده‌های فعلی، قادر است ساختار را تشخیص داده و گزارش دهد.

از گزارش فوق مشخص است که به دلیل تعیین نشدن سایز ورودی (Input Shape) این لایه آورده نشده است. در سطر اول مشخص شده یک لایه SimpleRNN به ابعاد نامشخص (None) و 64 داریم که به‌ترتیب نشان‌دهنده‌ی سایز Mini-Batch و سایز بردار حافظه نهان (Hidden State) است. در سطر دوم مشخص شده که در آخر شبکه به یک لایه تمام-متصل به ابعاد نامشخص و 1 می‌رسد.

بررسی تعداد پارامتر‌های آموزشی

تعداد پارامتر‌های قابل آموزش لایه بازگشتی به تعداد نورون‌های واحد بازگشتی (سایز حافظه نهان [Hidden State]) وابسته بوده و به تعداد تکرار واحد بازگشتی ارتباطی ندارد چرا که در واقع یک واحد بازگشتی تکرار شده و وزن‌ها در تکرارهای آن ثابت هستند.

در مسئله‌ی ما، ورودی شبکه یک بردار یک عنصری است (هر داده تنها یک فیچر (Feature) داشته و یک عدد بود) و طول واحد بازگشتی برابر 64 است. بنابراین، با توجه به معادلاتی که در جلسه‌ی پیش بررسی کردیم، تعداد پارامتر‌های آموزشی مدل به‌صورت زیر خواهد بود:

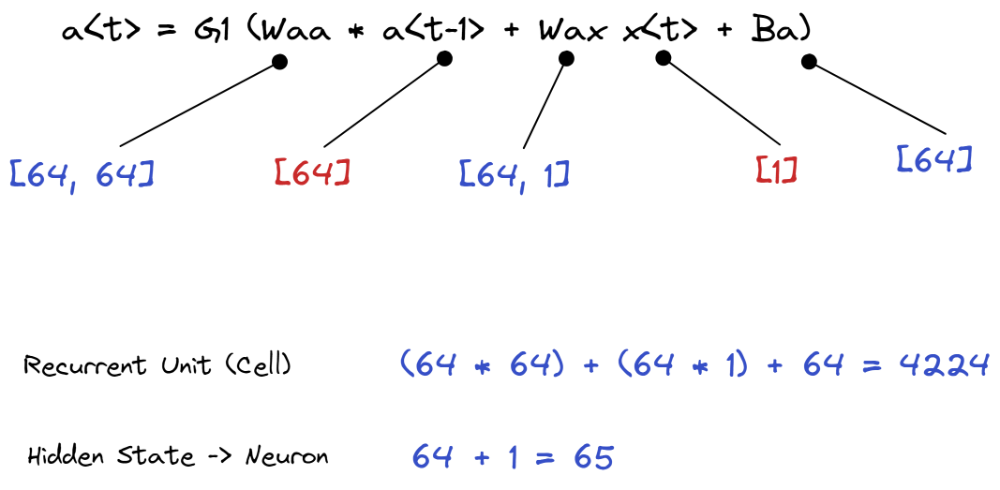
بنابراین، 4224 پارامتر در لایه بازگشتی (SimpleRNN)‌ و 65 پارامتر برای لایه تمام-متصل (Dense) در اختیار خواهیم داشت.

علاوه‌بر ساختار مدل، برای تشخیص ابعاد تنسور (Tensor) ورودی شبکه، می‌توانیم از ویژگی input داخل مدل استفاده کنیم:

که نتیجه آن به‌صورت زیر قابل مشاهده‌ست:

که در قسمت shape مشخص شده که ابعاد ورودی به‌صورت نامشخص (تعداد نمونه‌ها [سایز Mini Batch]) در 10 (تعداد گام‌زمانی‌ها) در 1 (تعداد فیچر‌های هر نمونه) است.

ارزیابی مدل

پس از آموزش مدل روی داده‌های آموزش خود، برای درک بهتری از عملکرد آن، می‌توانیم با رسم نمودار‌هایی مانند نمودار تغییرات زیان (Loss) بر حسب تعداد دوره‌ها (Epoch) و تجسّم پیش‌بینی‌ها در فاز‌های آموزش و آزمون، مدل را بررسی کنیم.

رسم نمودار تغییرات زیان (Loss) در طول دوره‌ها (Epochs)

برای رسم نمودار تغییرات زبان، با استفاده از کتاب‌خانه matplotlib که در ابتدای نوت‌بوک وارد کرده بودیم، به‌صورت زیر عمل می‌کنیم:

loss = history.history['loss']
plt.plot(loss, label='Training loss')
plt.legend()

plt.show()

با اجرا تکه کد بالا، نمودار تغییرات زیان بر حسب دوره‌ها دور طول آموزش مدل قابل مشاهده خواهد بود:

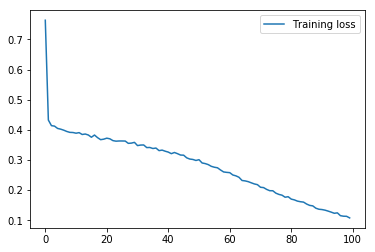
همانطور که مشخص است، نمودار تغییرات زیان مدل نزولی بوده و کاهش قابل توجهی داشته.

رسم سری‌های اصلی و پیش‌بینی (برای داده‌های آموزش و آزمون)

برای بررسی دقیق‌تر نحوه‌ی عملکرد مدل، داده‌های آموزش و آزمون را برای پیش‌بینی به مدل داده و با نتایج مورد انتظار واقعی مقایسه می‌کنیم. برای اینکار همانند قطعه کد زیر، با فراخوانی متد predict مدل و ارسال لیست داده‌های آموزش و آزمون، نتایج پیش‌بینی‌های مدل به ازای هر داده در این لیست‌ها را دریافت کرده و در متغیر‌های مربوطه ذخیره می‌کنیم:

trainPredict = model.predict(trainX)
testPredict  = model.predict(testX)

به یاد داریم، از 1500 داده‌ای که به‌عنوان محموعه‌داده اصلی خود تولید کردیم، 1000 داده برای فاز آموزش (Train) و 500 داده برای فاز آزمون (Test) جدا کرده بودیم، در ادامه برای سهولت رسم نمودار لیست‌های پیش‌بینی‌های بدست آمده را با یکدیگر الحاق (Concat) کرده -تا یک لیست 1500 تایی مشابه مجموعه داده اولیه داشته باشیم- و سپس با استفاده از کتاب‌خانه matplotlib به‌صورت زیر رسم می‌کنیم:

Predicted = np.concatenate((trainPredict,testPredict),axis=0)

plt.plot(x)
plt.plot(predicted)
plt.axvline(len(trainX), c="r")
plt.show()

در قطعه کد بالا، ابتدا نمودار داده‌های واقعی مسئله (مجموعه داده ساختگی که در ابتدای جلسه ایجاد کردیم [متغیر x]) را با یک رنگ (آبی) در نمودار رسم می‌کنیم. سپس، پیش‌بینی‌های بدست‌ آمده را با رنگی دیگر (نارنجی) به نمودار اضافه و رسم می‌کنیم. در نهایت با استفاده از یک خط عمودی (قرمز رنگ) پیش‌بینی‌های داده‌های آموزش را از داده‌های آزمون جدا کرده و مشخص می‌کنیم.

در نتیجه، نمودار پیش‌بینی‌های مدل در مقایسه با داده‌های مجموعه اصلی به‌صورت زیر قابل رسم خواهد بود:

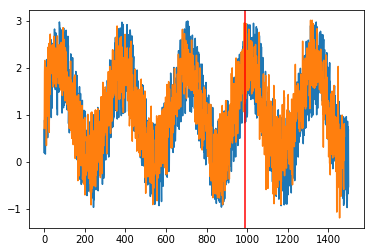
انتظار داشتیم، مدل در 1000 داده اول پیش‌بینی شده (Predict) که مربوط به داده‌های آموزش بوده و مدل پیش از این بارها آن‌ها را دریافت کرده عملکردی بی‌نقص داشته باشیم که همانطور که از قسمت سمت چپ خط عمودی قرمز در نمودار فوق مشخص است همین اتفاق افتاده‌ست.

همچنین، برای داده‌های تست، همانطور که از قسمت سمت راست خط عمودی قرمز مشخص است، مدل رگرسیون ما توانسته‌است نحوه عملکرد تابع سینوسی را به‌خوبی مدل کند.

.    .    .    .   .

در این جلسه در ادامه مباحث جلسه‌‌های قبلی، به پیاده‌سازی یک شبکه‌ی عصبی بازگشتی ساده با استفاده از کتاب‌خانه‌ی کراس (Keras) پرداخته، با شبکه‌ی SimpleRNN آن آشنا شده و مدل رگرسیونی برای پیش‌بینی روند یک تابع سینوسی آموزش دادیم. همچنین ساختار شبکه و پارامترهای آن را مورد بررسی قرار دادیم.

در جلسه‌ی بعدی به بررسی دقیق‌تر ابعاد ورودی‌های شبکه عصبی و نحوه‌ی استفاده و اجرای مدل برای ابعاد دیگر و گام‌زمانی‌های (timestep) متفاوت بحث خواهیم کرد.

می‌توانید لیست جلسات دوره را در این پست مشاهده کنید.

جلسه‌ی قبلی
جلسه‌ی بعدی (در دست انتشار)

.    .    .    .    .

این دوره به کوشش علیرضا اخوان‌پور به‌صورت ویدئویی تهیه شده و به قلم محمدحسن ستاریان با نظارت ایشان به‌صورت متنی نگارش و توسط بهار برادران افتخاری ویرایش شده‌ست.